[개념]기초 정렬 알고리즘
기초 정렬 알고리즘 🎰
✍ 기초 정렬 알고리즘
1️⃣ 선택 정렬
2️⃣ 삽입 정렬
3️⃣ 버블 정렬
4️⃣ 퀵 정렬
5️⃣ 계수 정렬 … 등 등
1️⃣선택 정렬
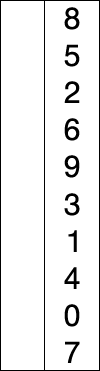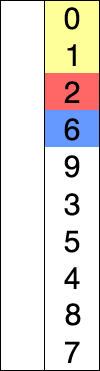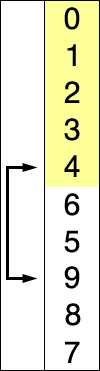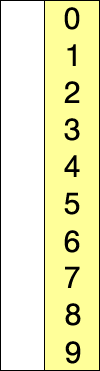
다음 gif와 같이
- 첫번째를 데이터를 제외한 뒷 부분중 가장 작은 데이터를 첫번째 데이터와 위치를 바꾼다.
- 두 번째 데이터와 두번째의 뒷부분 데이터중 가장 작은 데이터와 위치를 바꾼다.
- 세 번째 데이터와 세번째의 뒷부분 데이터중 가장 작은 데이터와 위치를 바꾼다.
- . . . . (반복) . . . .
파이썬을 이용한 구현
# 선택정렬
num = [5,8,1,7,9,2,4,6,3,10]
for i in range(len(num)):
min_index = i
for j in range(i+1,len(num)):
if num[min_index] > num[j]:
min_index = j
#스와프
num[min_index], num[i] = num[i], num[min_index]
#출력
num
»output
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2️⃣ 삽입 정렬
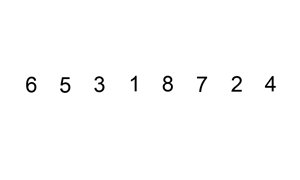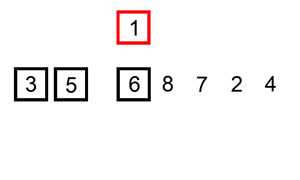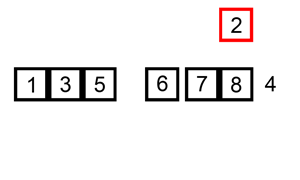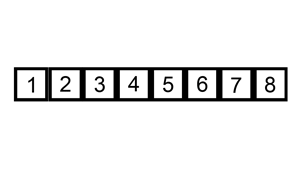
다음 gif와 같이
- 두 번째 데이터부터 시작합니다.
- 자신의 앞에 있는 데이터들과 비교하여 자신보다 작은 숫자 뒤에 삽입합니다.
- 세 번째 데이터를 자신의 앞에 있는 데이터들과 비교하여 자신보다 작은 숫자 뒤에 삽입합니다.
- . . . . (반복) . . . .
파이썬을 이용한 구현
# 삽입정렬
num = [5,8,1,7,9,2,4,6,3,10]
for i in range(1,len(num)):
for j in range(i,0,-1):
if num[j] < num[j-1]:
num[j],num[j-1] = num[j-1],num[j]
#출력
num
»output
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
3️⃣ 버블 정렬
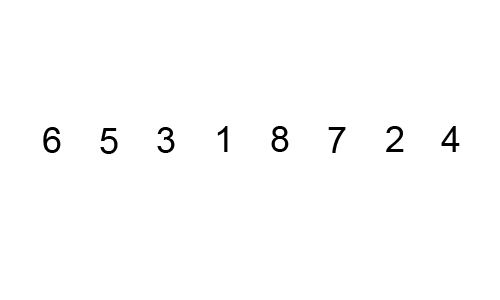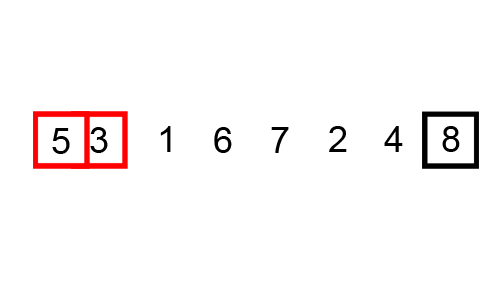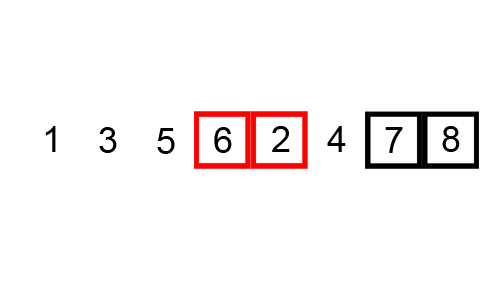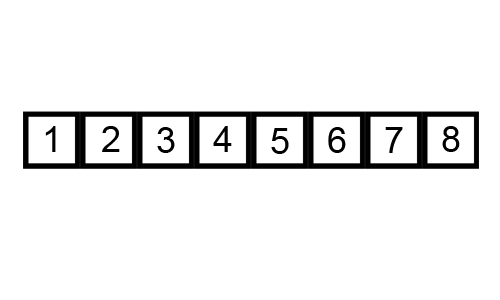
다음 gif와 같이
- 첫 번째 데이터와 두 번째 데이터를, 두 번째 데이터와 세 번째 데이터, 세 번째데이터와 네 번째 데이터를 비교하여 정렬을 시켜줍니다.
- 이 작업을 1회전하면 데이터중 가장 큰값은 제일 뒤로간다.
- . . . . (반복) . . . .
파이썬을 이용한 구현
# 버블정렬
num = [5,8,1,7,9,2,4,6,3,10]
for i in range(len(num)-1):
for j in range(len(num)-1-i):
if num[j] > num[j+1]:
num[j],num[j+1] = num[j+1],num[j]
#출력
num
»output
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
4️⃣ 퀵 정렬
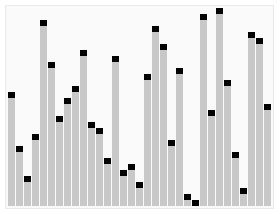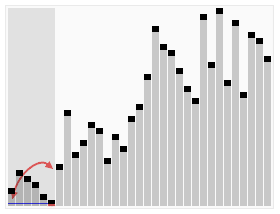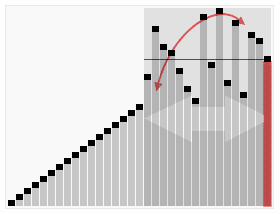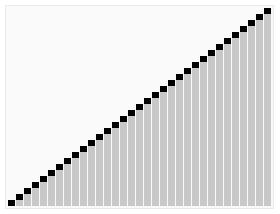
다음 gif와 같이
- 첫 번째 값을 pivot값을 정하고, 이를 기준으로 왼쪽부터 pivot보다 큰값 ,오른쪽부터 pivot보다 작은 값을 찾는다.
- 찾은 값들의 위치를 바꿔준다.
- 찾는 값의 인덱스가 교차 될때 까지 2번의 과정을 반복한다.
- 교차되는 인덱스는 위치를 바꿔주지 않고 pivot을 교차점 사이에 넣는다.
- pivot을 기준으로 왼쪽 리스트와 오른쪽리스트를 1~3 과정을 다시 반복한다. (재귀함수 활용)
파이썬을 이용한 구현
#퀵정렬
num = [5,8,1,7,9,2,4,6,3,10]
def quick_sort(num,start,end):
if start >= end:
return
pivot = start
left = start+1
right = end
while left <= right:
#피벗보다 작은 값의 인덱스를 찾을 때 까지 반복
while left <= end and num[left] <= num[pivot]:
left+=1
#피벗보다 큰 값의 인덱스를 찾을 때 까지 반복
while right > start and num[right] >= num[pivot]:
right-=1
# 인덱스가 엇갈린다면?
if left > right:
num[right],num[pivot] = num[pivot],num[right]
else:
num[left],num[right] = num[right],num[left]
quick_sort(num,start,right-1)
quick_sort(num,right+1,end)
quick_sort(num,0,len(num)-1)
num
»output
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
파이썬의 장점을 살린 퀵정렬
#퀵정렬
num = [5,8,1,7,9,2,4,6,3,10]
def quick(num):
if len(num) <= 1:
return num
pivot = num[0]
tail = num[1:]
left_side = [x for x in tail if x <= pivot]
right_side = [x for x in tail if x > pivot]
return quick(left_side)+[pivot]+quick(right_side)
quick(num)
»output
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
5️⃣ 계수 정렬
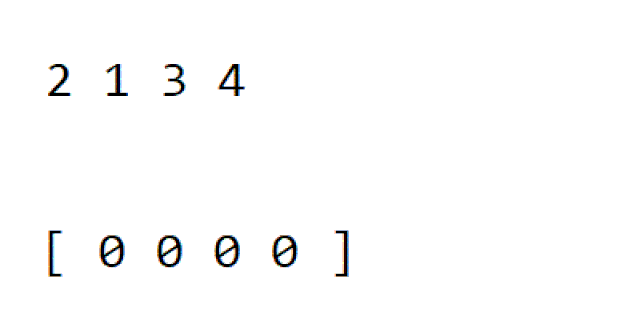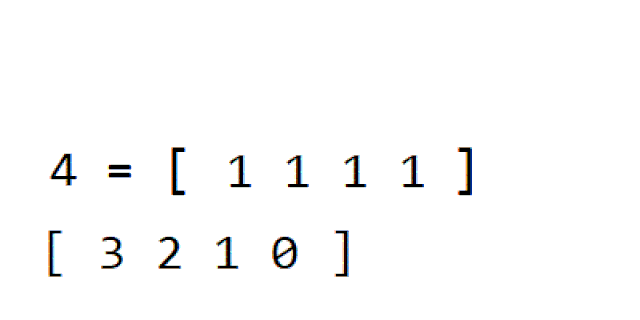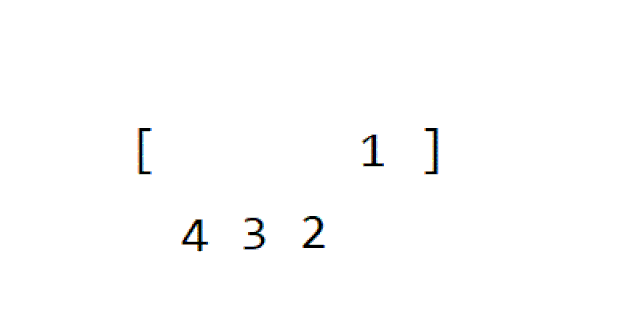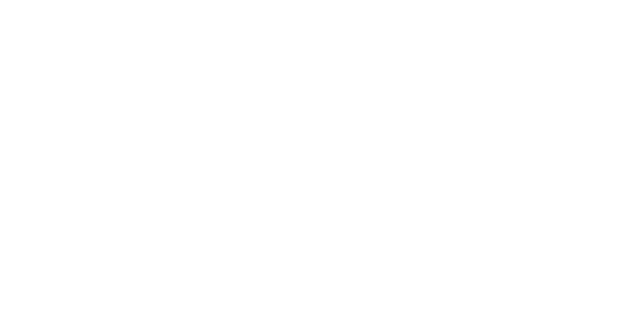
다음 gif와 같이
- 제일 작은 값과 제일 큰 값 사이에 값들을 가지는 리스트를 만듭니다.
- 위에서 만든 리스트값에 등장하는 데이터수를 저장합니다.
- 차례로 리스트의 인덱스를 값의 크기만큼 반복하여 나타냅니다.
파이썬을 이용한 구현
#계수 정렬
num = [5,8,1,7,9,2,4,6,3,10]
counter = [0]*max(num)+1
for i in num:
counter[num] += 1
for i in range(max(num)+1):
if counter[i]!=0:
for j in range(counter[i]):
print(i)
»output
1
2
3
4
5
6
7
8
9
10
✍정렬 알고리즘의 시간 복잡도 와 공간 복잡도
| 정렬 알고리즘 | 시간 복잡도 | 공간 복잡도 | |
|---|---|---|---|
| 🟥최선, 🟦최악, 🟩평균 | 최악 | ||
| 선택 정렬 (Selection sort) | 🟥O($n^2$) , 🟦O($n^2$), 🟩 O($n^2$) | O($n^2$) | |
| 삽입 정렬 (Insertion sort) | 🟥O(n) , 🟦O($n^2$), 🟩 O($n^2$) | O(n) | |
| 버블 정렬 (Bubble sort) | 🟥O($n^2$) , 🟦O($n^2$), 🟩 O($n^2$) | O(n) | |
| 퀵 정렬 (Quick sort) | 🟥O(n x $logn$) , 🟦O($n^2$), 🟩 O(n x $logn$) | O(n x $logn$) | |
| 계수 정렬 (Counter sort) | 🟩 O(n+k) (k는 데이터의 최댓값) | O(n+k) |
✍정렬 알고리즘의 장단점
| 정렬 알고리즘 | 장점😊 | 단점😥 | |
|---|---|---|---|
| 선택 정렬 (Selection sort) | 구현이 쉽다. | 시간이 오래걸려서 비효율적이다. | |
| 삽입 정렬 (Insertion sort) | 최선의 경우 O(N)이라는 빠른 속도를 낼수 있다. 성능이 좋아 다른 정렬법에도 일부 사용된다. | 최악의 경우 O($n^2$) | |
| 버블 정렬 (Bubble) | 구현이 쉽다. | 시간이 오래걸리고 효율성이 좋지 않다. | |
| 퀵 정렬 (Quick sort) | 매우 빠른 속도를 가지고 있다. O(N x $logN$) | pivot에 의해서 성능차이가 난다. 최악의 경우 O($n^2$) | |
| 계수 정렬 (Counter) | 매우 빠른 속도를 가지고 있다. O(N) | 메모리 공간이 많이 쓰인다. (일부 값때문에 많이 낭비 될 수 있음) |
이것이 코딩 테스트다 - 나동빈 저
댓글남기기