[백준][python] 2579번: 계단 오르기

2579번: 계단오르기

• 백준(boj) 2579번

문제

계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다.

<그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

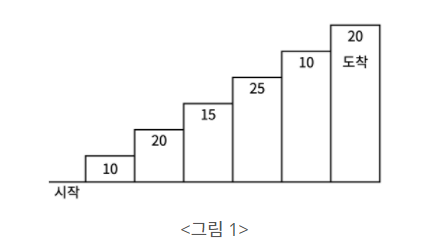
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아

도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

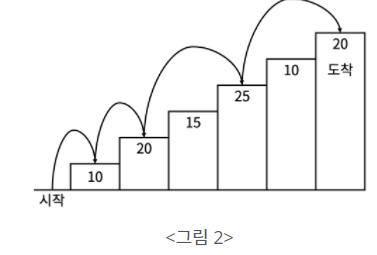
계단 오르는 데는 다음과 같은 규칙이 있다.

1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
3. 마지막 도착 계단은 반드시 밟아야 한다.

따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다.

하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.

각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.

입력 조건

입력의 첫째 줄에 계단의 개수가 주어진다.

둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다.

계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.

출력 조건

첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

첫 번째 시도 .

step = int(input())

score = [0]
for _ in range(step):
    score.append(int(input()))

d=[0]*301

d[1]=score[1]
d[2]=score[1] + score[2]

if step==1:
    print(d[1])
else:
    for i in range(3,step+1):
        d[i] = max(score[i] + score[i-1] + d[i-3],score[i] + d[i-2])
    print(d[step])

»intput

6
10
20
15
25
10
20

»output

75

fail

🌝 Thinking

최적 해를 구하는 문제임으로 다이나믹 프로그래밍 알고리즘을 이용해야한다.

i 번째 계단까지의 최적 해 =

1. i번째 요소 + (i - 1)번째 요소 (i - 3)번째 까지의 최적 해
2. i번째 요소 + (i - 2)번째 까지의 최적 해

1️⃣과 2️⃣ 중 큰 값!!

라는 점화식을 Bottom up 방식으로 구현을 해보았다.

이 점화식 아이디어를 떠오르는 데까지 15분 정도의 시간이 소요 되었는데,

시간이 조금 걸렸던 이유는 지금까지 내가 만나본 문제들은 점화식을 만들기 위한

인접 항들이 -2 번째 항 안에서 다 해결이 되었기 때문에 조금 고착된 사고를 한 것 같다.

…

엥? Index Error ? why?

---

두 번째 시도 .

step = int(input())

score = [0]
for _ in range(step):
    score.append(int(input()))

d=[0]*301

if step==1:
    print(score[1])
else:
    d[1]=score[1]
    d[2]=score[1] + score[2]
    for i in range(3,step+1):
        d[i] = max(score[i] + score[i-1] + d[i-3],score[i] + d[i-2])
    print(d[step])

»intput

6
10
20
15
25
10
20

»output

75

success

🌝 Thinking

다이나믹 프로그래밍 알고리즘을 Bottom Up 방식으로 구현하다 보면 for구문으로 점화식을 자주 구현하게 된다.

이때 점화식은 주로 인접항과의 관계로서 만들어지는데 점화식 스타트가 되는 초깃값에 대한 부분은 for 구문에서

빠지게 된다. (for 구문 3부터 출발)

for 구문은 step + 1 까지 순회하게 되는데 보통 다이나믹 프로그랭을 짤 때 저 step자리가 우리가 구하고자는

번째(index)가 된다. 만약 이 값이 3보다 작을 경우 Index Error가 일어난다.

---

💡 깨달은 점.

1. 다이나믹 프로그래밍 Bottom Up 을 이용한 구현에서 Index Error가 일어나지 않도록 예외 사항을 따로 고려해 주어야 한다.