3 분 소요

1260번: DFS와 BFS

🔥DFS/BFS 연습문제

문제

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오.

단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고,

더 이상 방문할 수 있는 점이 없는 경우 종료한다.

정점 번호는 1번부터 N번까지이다.

입력

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다.

다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다.

어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

출력

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다.

V부터 방문된 점을 순서대로 출력하면 된다.

예제

4 5 1
1 2
1 3
1 4
2 4
3 4

예제 출력

1 2 4 3
1 2 3 4

🌝 Thinking

  1. 입력을 간선(무방향)이 연결하는 두 번호를 준다.
  2. 간선이 열결하는 두 번호 👉 인접행렬 OR 인접리스트 로 만들어 주어야한다.
  3. 인접 행렬과 인접리스트를 이용하여 DFS/BFS를 구현한다.

❓인접행렬 은 어떻게 만들까?

n,m,v = map(int,input().split())

#우선 (노드수+1) x (노드수+1) 크기의 정사각행렬을 만든다.
graph = [[0]*(n+1) for _ in range(n+1)]

#x,y 간선이 연결한 두번호가 정사각행렬의 인덱스이고, 그 행렬의 요소가 연결상태를 나타낸다.
for i in range(m):
    x,y = map(int,input().split())
    graph[x][y] = 1
    graph[y][x] = 1

#정사각행렬 출력해보기.
for row in graph:
    print(row)

output

[0, 0, 0, 0, 0] 
[0, 0, 1, 1, 1] #노드1
[0, 1, 0, 0, 1] #노드2
[0, 1, 0, 0, 1] #노드3
[0, 1, 1, 1, 0] #노드4

다음과 같이 인접행렬이 잘 만들어지는 모습을 확인할 수 있다.

간선이 연결한 두 번호가 인접행렬에서의 요소(연결성 확인요소) 의 인덱스가 된다.

인접행렬 을 이용한 나의 풀이

n,m,v = map(int,input().split())

#인접행렬을 만듬.
graph = [[0]*(n+1) for _ in range(n+1)]
for i in range(m):
   x,y = map(int,input().split())
   graph[x][y] = 1
   graph[y][x] = 1
#방문확인 리스트제작.
visited_dfs = [False]*(n+1)
visited_bfs = [False]*(n+1)

#DFS 만들기
def dfs(v):
   visited_dfs[v] = True
   print(v,end=' ')
   
   #만약 그래프가 연결이되어 있고, 방문하지 않은 상태라면 ?
   for i in range(n+1):
       if graph[v][i] == 1 and not visited_dfs[i]:
           #위의 과정을 반복하시오.
           dfs(i)
           
#BFS 만들기
from collections import deque

def bfs(v):
   queue = deque([v])
   visited_bfs[v] = True
   
   while queue:
       v = queue.popleft()
       print(v,end=' ')
       for i in range(n+1):
           if graph[v][i]==1 and not visited_bfs[i]:
               queue.append(i)
               visited_bfs[i] = True

#입출력 형식 맞추기.
dfs(v)
print()
bfs(v)

output

1 2 4 3 
1 2 3 4

그림으로 확인

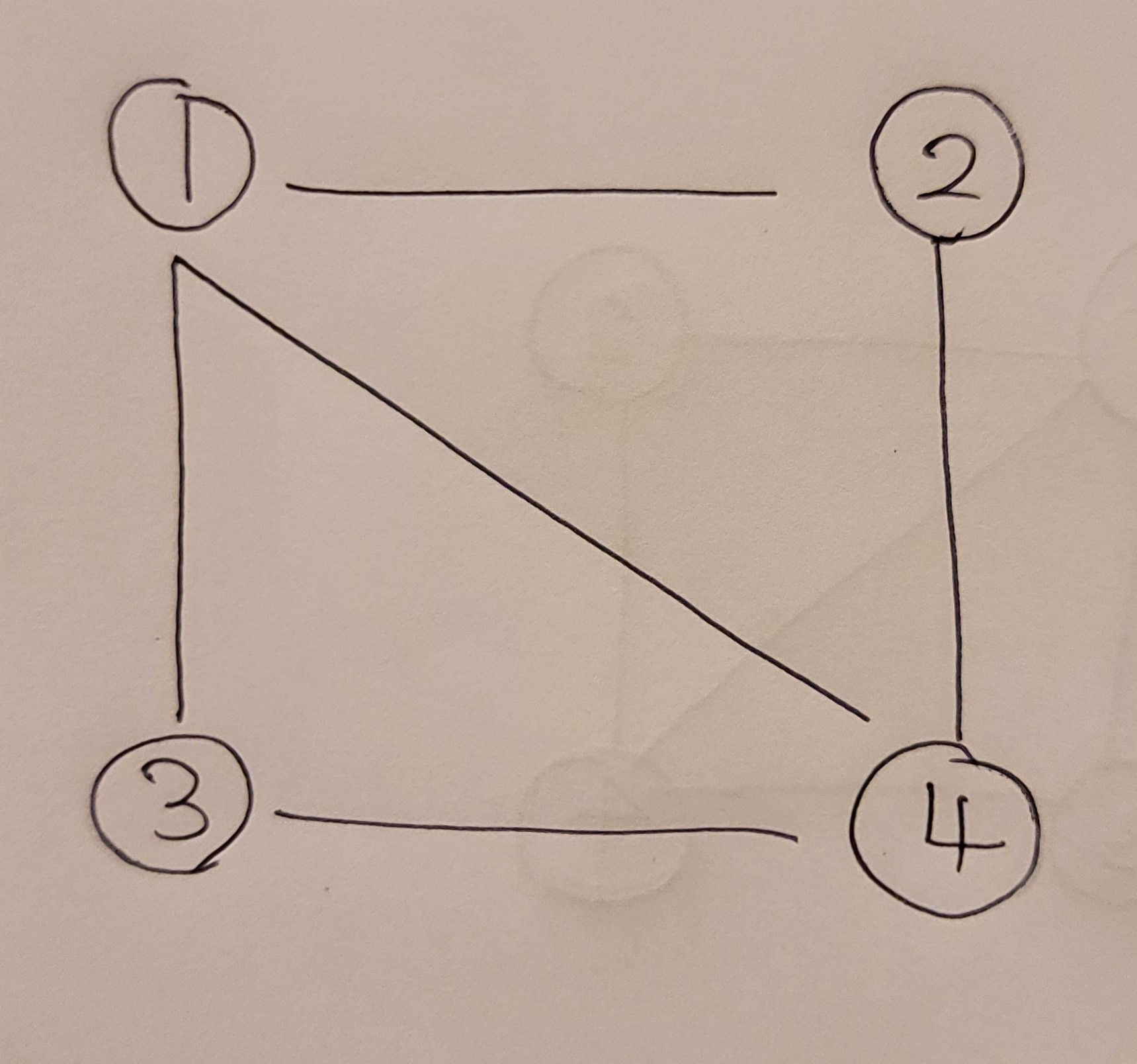
KakaoTalk_20220213_224710608



통과완료!!!!@@@@@

image-20220213225010760








그렇다면…?




❓인접리스트를 어떻게 만들까?

n,m,v = map(int,input().split())

graph=[[] for _ in range(n+1)]

#graph[x]는 노드x를 말하고 간선으로 y와 연결되어있으므로 y를 리스트에 담는다
#graph[y] 또한 마찬가지
for i in range(m):
    x,y = map(int,input().split())
    graph[x].append(y)
    graph[y].append(x)

print(graph)

output

[[], [2, 3, 4], [1, 4], [1, 4], [1, 2, 3]]
#       노드1     노드2   노드3      노드4

다음과 같이 인접리스트가 잘 만들어지는 모습을 확인할 수 있다.

간선으로 연결이되어 있다는건 한쪽 노드를 기준을 잡고 다른 노드와 연결되어있다는 접근

인접리스트를 이용한 나의 풀이

n,m,v = map(int,input().split())

#인접리스트 제작.
graph=[[] for _ in range(n+1)]
for i in range(m):
x,y = map(int,input().split())
graph[x].append(y)
graph[y].append(x)

#방문확인 리스트제작.
visited_dfs = [False]*(n+1)
visited_bfs = [False]*(n+1)

#DFS 만들기.
def dfs(v):
visited_dfs[v] = True
print(v, end=' ')
for i in graph[v]:
   if not visited_dfs[i]:
       dfs(i)

#BFS 만들기.
from collections import deque

def bfs(v):
queue = deque([v])
visited_bfs[v]=True
while queue:
   v = queue.popleft()
   print(v,end=' ')
   for i in graph[v]:
   	if not visited[i]:
	        	queue.append(i)
       	visited_bfs[i] = True

#입출력 형식 맞추기.
dfs(v)
print()
bfs(v)

output

1 2 4 3 
1 2 3 4

인접리스트로도 구현 완료!




🟧인접행렬 vs 🟦인접리스트

🟧인접행렬 장점 👍

  1. 2차원 배열의 모든 정점들의 간선 정보가 있다.

    두 정점을 연결하는 간선을 조회할 때, O(1) 시간 복잡도로 가능하다.

    (인덱스로 바로 찾으면 됌)

  2. 정점(i)의 차수를 구할 때 인접행렬의 i번째 행의 값을 모두 더하면 된다. O(n)의 시간 복잡도를 가진다.

🟧인접행렬 단점👎

  1. 2차원 배열을 사용함으로 메모리 공간이 낭비된다.
  2. 간선의 수를 모두 알아내기 위해서는 인접행렬 전체를 확인해야 된다. O(n^2)의 시간 복잡도를 가진다.

🟦인접리스트 장점 👍

  1. 간선만 관리하면 되므로 메모리 공간 활용이 효율적이다.

  2. 모든 간선의 수를 알아내기 위해 각 정점의 헤더 노드 부터 모든 인접리스트를 탐색해야하므로 O(n+e)의 시간이 소요된다.

🟦인접리스트 단점👎

  1. 두정점을 연결하는 간선을 조회 하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 정점의 차수만큼 시간이 필요하다. O(degree(v))
  2. 구현이 어렵다.


출처/참고

Suyeon’s Blog

댓글남기기

참고